HW#6 Ch 2: Motion Along a Straight Line
1. The velocity of a particle is given by v = 4t − 4, where t is in seconds and v is in meters per second. a) Sketch v(t) versus t using graph paper, and find the area under the curve (using area formulae for triangles, rectangles or trapezoids) for the interval t = 0 to t = 4s. b) Find the position function x(t) by integration, assuming that x(0) = 2m. Use it to calculate the displacement during the interval t = 0 to t = 4 s.
2. The velocity of a particle is given by v=4t3 − 2, where t is in seconds and v is in meters per second. Find the general position function x(t).
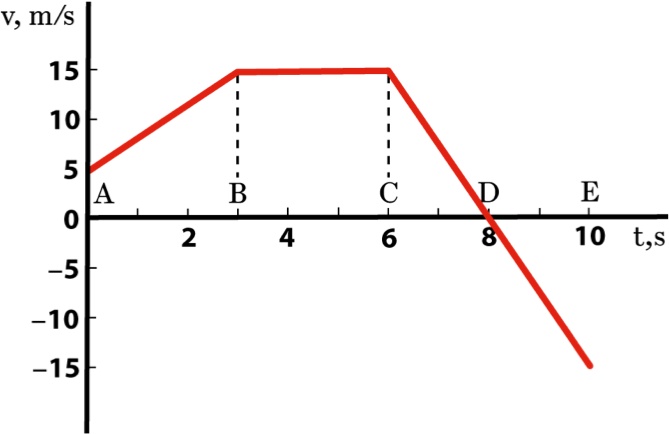
3. Consider the velocity graph in the figure below for a particle with initial position x = 0 at time t = 0. a) Using the appropriate formula, determine the acceleration in regions AB, BC and CE from the slope of the line. b) Write the equation for v(t) in regions AB, BC and CE by using the point-slope formula (equation of a line). c) Write the equation for x(t) in regions AB, BC and CE by integrating the velocity with respect to time. Use the given boundary conditions to solve for any constants that arise.
4. The acceleration of a certain rocket is given by a = Ct2, where C is a constant. a) Find the general position function x(t). b) Find the position and velocity at t = 5 s if x = 0 and v = 0 at t = 0 and C = 3 m/s4.
