HW#31 Ch 11: Conservation of Angular Momentum
Instructions: Be sure to write formulas and show substitutions to earn full credit.
1. Ryan wants to build a car for his pet mouse, Mickey, so that he can impress his mouse girlfriend, Minnie. Ryan decides to use a Kerrygold Cheddar cheese wheel for a tire, so that the mice couple will have something to eat if they get hungry. Assume that each cheese wheel is a uniform disk of 17.78 cm in diameter and weighs 11.0 kg. Two cheese wheels are joined by a wooden cylinder of 2.54 cm in diameter and 30.5 cm in length, so that the wooden cylinder (axle) is firmly embedded in each cheese wheel at the center. Neglect the weight of the wooden axle and the weight of the cheese removed to insert the axle. The cheese wheel/axle system rolls down a 2-m high ramp without slipping such that only the axle is in contact with the ramp. a) Calculate the moment of inertia of the cheese wheels in SI units. b) Calculate the ratio of rotational kinetic energy to translational kinetic energy as the cheese wheels roll down the ramp on its axle.
2. A solid marble of uniform density rolls down an inclined ramp without slipping, accelerating at a rate of 0.25 g. What is the angle of the ramp in degrees? You must derive the equation using torque equations, including a proper FBD.
3. A baseball of mass m is hit with speed v at an angle θ above the horizontal, such that it is influenced only by gravity. a) Write the displacement vector and linear momentum vector for the baseball as a function of time in terms of m, v, θ, and fundamental constants. b) Find the angular momentum vector as a function of time by taking the cross product of the displacement and momentum vectors. c) Find the torque by taking the derivative of angular momentum with respect to time.
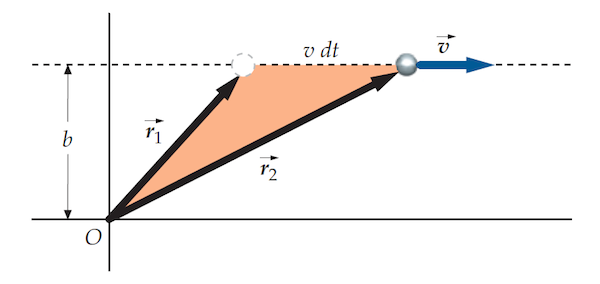
4. A hockey puck is traveling with a constant velocity \(\vec v \) along a line that is a distance b from a player at the origin O (see figure below). Let dA be the area swept out by the position vector from O to the particle in time dt. Show that \(\dfrac{dA}{dt}\) is constant in time and equal to \(\dfrac{L}{2m}\), where L is the angular momentum of the particle about the origin.