HW#15 Ch 5: Force and Motion — I
Instructions: Show all work using Newton’s 2nd law and free body diagrams.
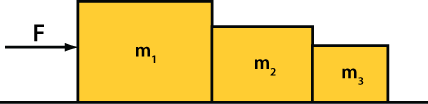
1. Three boxes, of mass m1 = 6 kg, m2 = 4 kg and m3 = 2 kg rest on a horizontal frictionless surface as shown in the image below. A force of 36 N is applied to the 6 kg box. a) What is the acceleration of all three boxes? b) What are the three normal forces on the 4 kg box as it accelerates to the right?
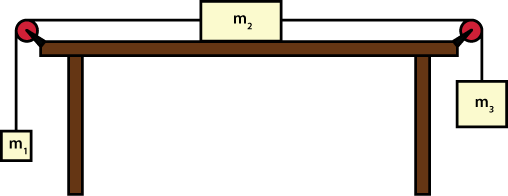
2. A box of mass m2 rests on a horizontal frictionless table (see attached figure). Two additional boxes, of masses m1 and m3, hang vertically from ropes that are attached to box m2. The ropes pass over two massless pulleys with frictionless bearings. If m1 = 2.1 kg, m2 = 7.4 kg and m3 = 5.5 kg, find a) the acceleration of the blocks and b) the tensions T1 and T2 in each rope.
3. You are the chief engineer responsible for designing the elevators in a luxury high-rise apartment. Inside each elevator is a 20 kg chandelier suspended by a cord rated at a maximum tension of 300 N. The residents wish to reach their apartments as quickly as possible, but they don’t wish to become crushed by a heavy chandelier. If you accelerate at a constant rate to a point midway to the top of the building, then decelerate at the same constant rate until you reach a standstill 40 m above the ground, what is the minimum time that the elevator is in operation without breaking the cord?
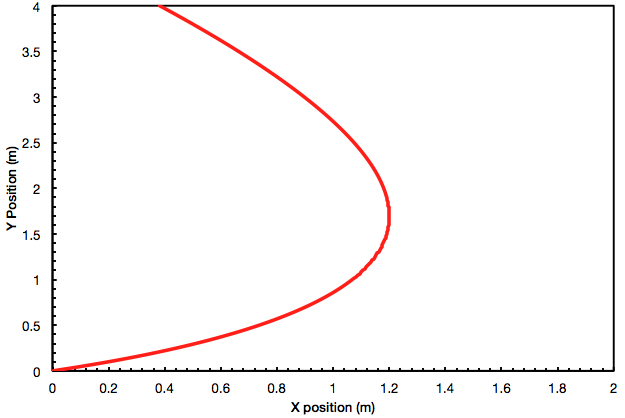
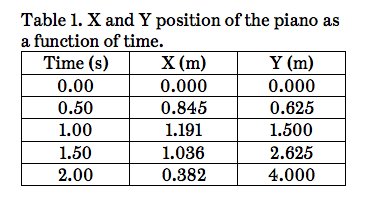
4. A 345-kg Steinway B piano starts rolling across the floor before two workers run over to intercept it. One worker pushes toward the west window (corresponding to the −X direction in Figure 4) and another worker pushes toward the north window (corresponding to the Y direction). Eventually they guide it out the door and down the ramp of the house. Using the data in Table 1 below, what is the net force, in unit vector notation, assuming that both workers apply a constant force to the piano? Hint: one way to solve this problem is to analyze x vs. t and y vs. t separately to find the components of the acceleration. In Excel, fit each graph with a least-squares polynomial regression of order 2. (Plotting x vs. t2 or y vs. t2 won’t work here because there is an initial velocity.)