HW#20 Ch 7: Kinetic Energy and Work
Instructions: Show your work by writing formulas and showing substitutions to earn full credit.
1. Kaveh owns a cabin in the woods that is a bird lover’s paradise; birds come from all over the area to bathe in his luxurious birdbath. To fill the birdbath, Kaveh has a bucket that has a mass of 10 kg that holds 30 kg of water when full. Much to Kaveh’s chagrin, he discovers that there is a hole in the bucket. Dear Liza! Because he ascends the ladder at constant speed, water leaks out at a constant rate. When Kaveh arrives at the top of the ladder, which is 20 m above the ground, he finds that there is only 10 kg of water left in the bucket. (a) Write an expression for the mass of the bucket and water as a function of the height y that he climbs. (b) Find the work done by Kaveh on the bucket.
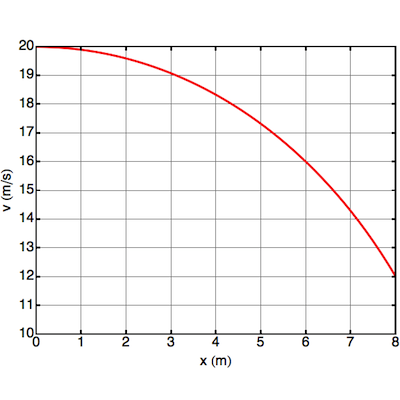
2. A 1 kg copper sphere is initially moving to the right at time t = 0, when it experiences a retarding force. If its velocity as a function of position is shown in the diagram below, how much work is done on the sphere from x = 0 to x = 8 m?
3. A 2.4 kg box is lifted by a force equal to the weight of the box. The box moves upward at a constant velocity of 2 m/s. (a) What is the power input of the force? (b) How much work is done by the force in 4 s?
4. Patrick’s cat has just caught a mouse, and he drags it across the floor so that Patrick can admire it. A constant horizontal force of 3 N is enough to drag the mouse across the rug at a constant speed v. If Patrick’s cat does work at the rate of 6 W, (a) what is his speed, v? (b) How much work does the cat do in 4 s?
5. Find the power input of a force acting on a particle that moves with a velocity \(\vec v\) for
a) \(\vec F = 4N \hat i + 3N \hat k\), \(\vec v = 6 \frac{{m}}{s} \hat i\)
b) \(\vec F = 6N \hat i - 5N \hat j\), \(\vec v = -5 \frac{{m}}{s} \hat i + 4 \frac{{m}}{s} \hat j\)
c) \(\vec F = 3N \hat i + 6N \hat j\), \(\vec v = 2 \frac{{m}}{s} \hat i + 3 \frac{{m}}{s} \hat j\)