HW#35 Ch 13: Gravitation
Instructions: Be sure to write formulas and show substitutions to earn full credit.
1. A protoplanet has a density that varies with distance as ρ(r) = ρ0(2 − r/R)2 where r is the radial distance, R is the radius of the protoplanet and ρ0 is a constant. The protoplanet has total mass M. Derive an expression for the gravitational field as a function of r, M and fundamental constants, for a) r < R and b) r > R.
2. If the Sun shrank with no change in mass, its gravitational acceleration would increase, as would its escape speed. What would the radius of the Sun have to be so that its escape speed would be the speed of light (c = 3 x 108 m/s)? Use Msun = 1.99 x 1030 kg. (Such an object is called a black hole. Note that the Sun is not large enough to become a black hole, so the question is purely hypothetical.)
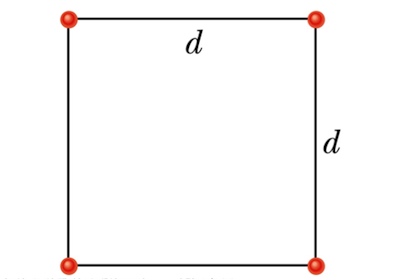
3. The figure below shows four balls, each of mass 454 g, that form a square with sides of length d = 0.500 m. What is the gravitational potential energy required to assemble the four balls in a square if they are originally very far apart?
4. Ceres, which is the largest object in the asteroid belt, is a dwarf planet made of rock and ice. It has a mass of 9.43 x 1020 kg and is 950 km in diameter. (a) What is the escape speed of a spaceship on Ceres? (b) How far will the spaceship go if it leaves the asteroid’s surface with an initial speed of 250 m/s? (c) With what speed will a spacesuit hit the asteroid if it is dropped from 1000 km above the surface?