HW#32 Ch 11: Conservation of Angular Momentum
Instructions: Be sure to write formulas and show substitutions to earn full credit.
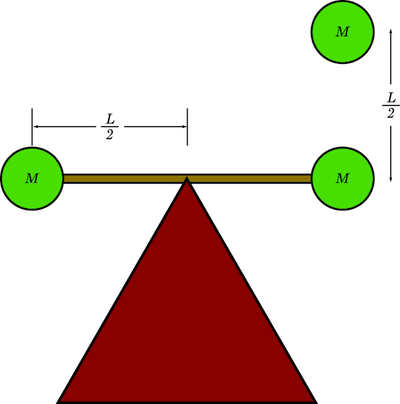
1. Two point masses of mass M are attached to the ends of a massless rod of length L. The rod is attached to a pivot at the center, so that it can freely swing around the pivot. The rod/point mass combination is initially balanced and at rest in a horizontal position. A third point mass of mass M is released from a height of L/2 above one of the point masses and undergoes an inelastic collision. The rod and three point masses begin to swing around the pivot. a) What is the angular speed when the rod is in a vertical position? b) Will the rod have enough energy to complete a full revolution? Justify your answer through calculations.
2. The figure below shows a top-down view of a rod of mass M and length L resting on a low-friction ice surface. A ripe piece of mango of mass m is flung at the rod with initial speed v, striking the rod at a 90° angle a distance d from the rod’s center. The mango piece sticks to the rod, and the two objects start moving and spinning simultaneously. (a) Find the center of mass of the rod/mango system relative to the bottom of the rod. (b) Calculate the moment of inertia of the rod/mango system about the center of mass. (c) Determine the velocity of the center of mass after the collision. (d) Find the angular speed after the collision.
3. A bicycle tire of mass 6.4 kg and radius 31.1 cm is suspended from a rope at the end of an axle a distance of 8 cm from the center of mass of the tire. Starting from rest, a constant torque of 1.8 N·m is applied for 10 seconds, giving the wheel an angular speed. Once you release the wheel, how long does it take for it to precess for a full revolution? Treat the tire as an ideal hoop and neglect friction.