HW#24 Ch 8: Potential Energy and Conservation of Energy
Instructions: Use an energy approach to solve these problems. Show your work by writing formulas and showing substitutions to earn full credit.
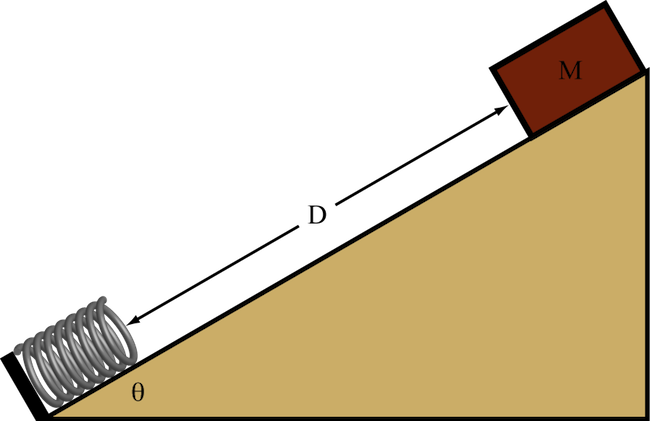
1. A block of mass M slides down a ramp with an angle of θ = 30° and a coefficient of kinetic friction of μk = 0.2, as pictured in the diagram below. The block collides with an elastic spring with spring coefficient k = 540 N/m at the bottom of the ramp. If the block has a mass M = 3.2 kg and it slides a distance D = 120 cm before touching the spring, a) by how much does the spring compress? b) What distance D′ does the block slide up the ramp before momentarily coming to rest?
2. A non-Hookian spring has a force that varies as F = −Cx2 instead of F = −kx. If the spring is compressed a horizontal distance x0, at what value of x would the potential energy of a block of mass m be equal to its kinetic energy? Express your answer in terms of x0.
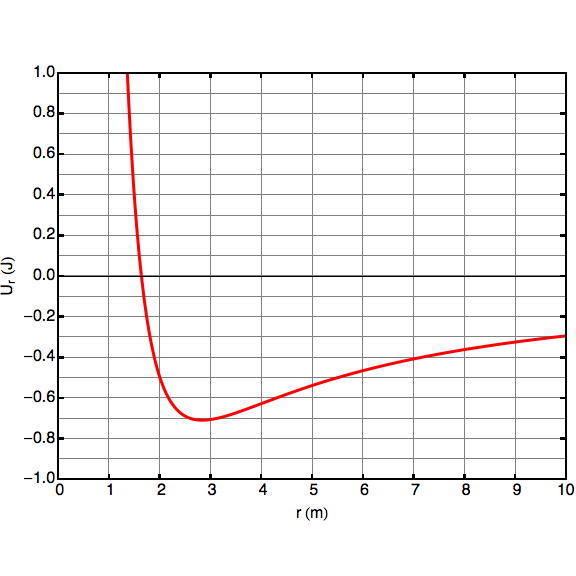
3. A 2 kg steel ball is placed in a frictionless asymmetric well, such that it rolls back and forth around an equilibrium point. Its potential energy function is given by \[U\left( r \right) = - \frac{3}{r} + \frac{8}{{{r^3}}}\] where r is in meters and U is in joules (see figure below). a) Find the value of r when the ball is at equilibrium. b) Show mathematically that this point is a stable equilibrium. c) If the velocity at the equilibrium is given by \[v = \sqrt {\frac{{\sqrt 2 - 1}}{2}} \frac{m}{s}\] find the values of r for which the ball is momentarily at rest. Express your answer in radical form. (This means you cannot use Solver -- the cubic equation can be solved simply by substituting r = y + 2.)