HW#38 Ch 15: Oscillations
Instructions: Be sure to write formulas and show substitutions to earn full credit.
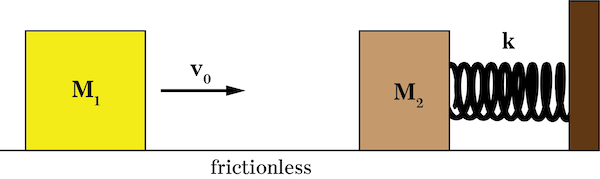
1. A block of mass M1 is traveling to the right at speed v0 on a frictionless surface when it encounters a block of mass M2 attached to a spring of spring constant k, initially at rest. Block M1 undergoes an inelastic collision with block M2, causing the combined masses to oscillate. a) What is the speed of the blocks after the collision, in terms of M1, M2 and v0? Assume that the spring is massless. b) What is the period of oscillation in terms of the given variables and fundamental constants?
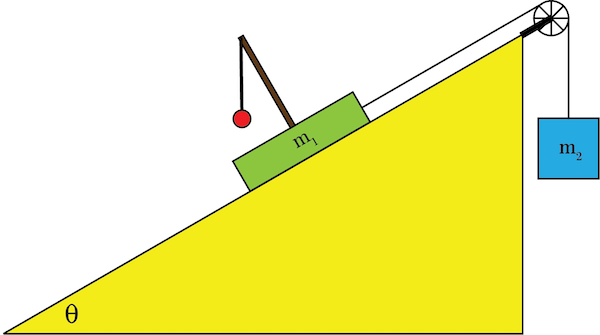
2. A simple pendulum is oscillating on top of a block of mass m1, which is resting on a frictionless incline at angle \(\theta \). Block m1 is attached to a block of mass m2 by a massless rope passing over an ideal massless pulley. Mass m2 is sufficiently heavy so that it accelerates downward. a) What is the acceleration of both blocks in terms of m1 and m2? Assume that the pendulum weight is negligible. b) If m1 = 1.5 kg, m2 = 1.2 kg and \(\theta\) = 20º, what is the period of the pendulum if the length of the string is 30 cm?
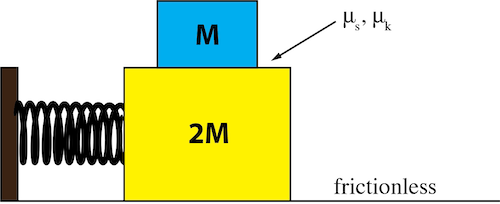
3. A block of mass 2M is attached to a spring of spring constant k and rests on a horizontal frictionless surface. The block is initially at rest. A block of mass M is stacked on top of the 2M block, and it is free to move across the surface of the lower block. The coefficient of static friction and kinetic friction between the two blocks are \(\mu _s\) and \(\mu_k \), respectively. a) If a force is applied to the left on the 2M block, what is the largest displacement of the spring such that the block M is on the verge of slipping? b) What is the period of oscillation if the amplitude is less than part a)? c) What is the period of oscillation if the top block slips off? d) What is the maximum acceleration and velocity if the amplitude is half that found in a)?
4. A simple pendulum of length \(L\) has a period of 2 seconds in an elevator that accelerates downward. If its length is increased by 2.5 feet under the same conditions, its period is 3 seconds. a) What is the length \(L\)? b) What is the acceleration of the elevator?