HW#22 Ch 8: Potential Energy and Conservation of Energy
Instructions: Use an energy approach to solve these problems. Show your work by writing formulas and showing substitutions to earn full credit.
1. A certain force varies with distance as F(x) = 2cos(2x), where x is in meters and F is in Newtons. Find the potential energy U(x) that corresponds to this force.
2. Speedy the chipmunk slides down a 2-m high curved frictionless ramp starting from rest. He continues to slide across a frictionless horizontal surface before colliding with a coiled spring with spring constant k = 38 N/m, compressing it a distance x before momentarily coming to rest. If Speedy has a mass of 130 g, (a) find the distance x.
For the following, indicate whether the quantities are increasing, decreasing or constant, maximum or minimum, and state the direction.
Describe the general motion of Speedy (velocity, acceleration) (b) at the point of maximum compression, (c) during the spring's rebound, (d) the moment Speedy leaves the spring, and (e) the curved section of the ramp. (f) Determine Speedy's height and acceleration when he is momentarily at rest.
3. The potential energy function for a rolling marble is represented by U(x,y) = 2xy3 – 5x + 2y, where x and y are in meters and U is in joules. Find the force in unit vector notation at the point (2,3).
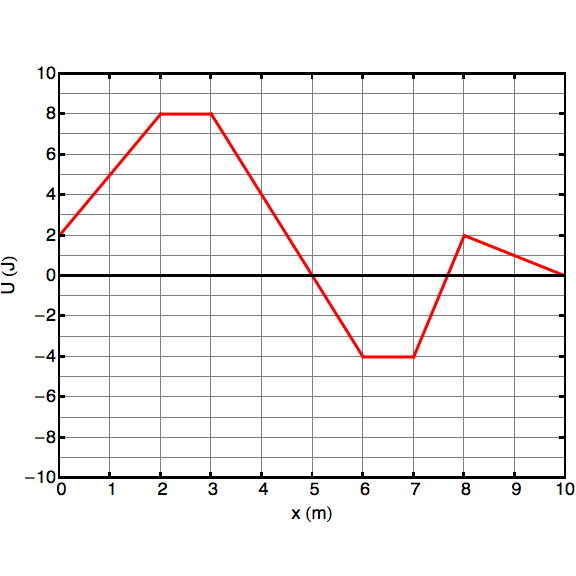
4. The graph below shows a plot of the potential energy of a toy car versus horizontal distance. a) Using graph paper, draw a plot of force versus distance x, making sure to label and number your axes. b) If the toy car has a mass of 1 kg and it has a speed of 2 m/s at x = 0, what is its speed at x = 10 m?